みなさん、こんにちは!今回は、公立高校入試に出そうな数学シリーズ第3回「基本の確率」の続きです。確率の応用問題は、公立高校入試でよく出題されるテーマの一つです。ですから、確率の応用問題の解き方も詳しく図説します。例題を一緒に解きながら、確率の解法のコツをつかんでくださいね!

応用問題やるよ

一緒に解こうね
第3回「基本の確率は」こちらです。
応用問題の解き方
それでは、応用問題に挑戦してみましょう。公立高校入試では、このような複合的な確率問題が出題されることがあるので一緒に解いてみましょう。最後には、何が複合的なのかがわかりますよ。
複合確率
この例題は、第3回の色付きボールの例題に似ていますが、もちろん、違います。つまり、その違いが解き方のヒントになります。
解き方のヒント
① 袋から、同時に2個のボールを取り出す。
② 組み合わせの公式
③ 同じ色を2個選ぶときも注意
例題
問題
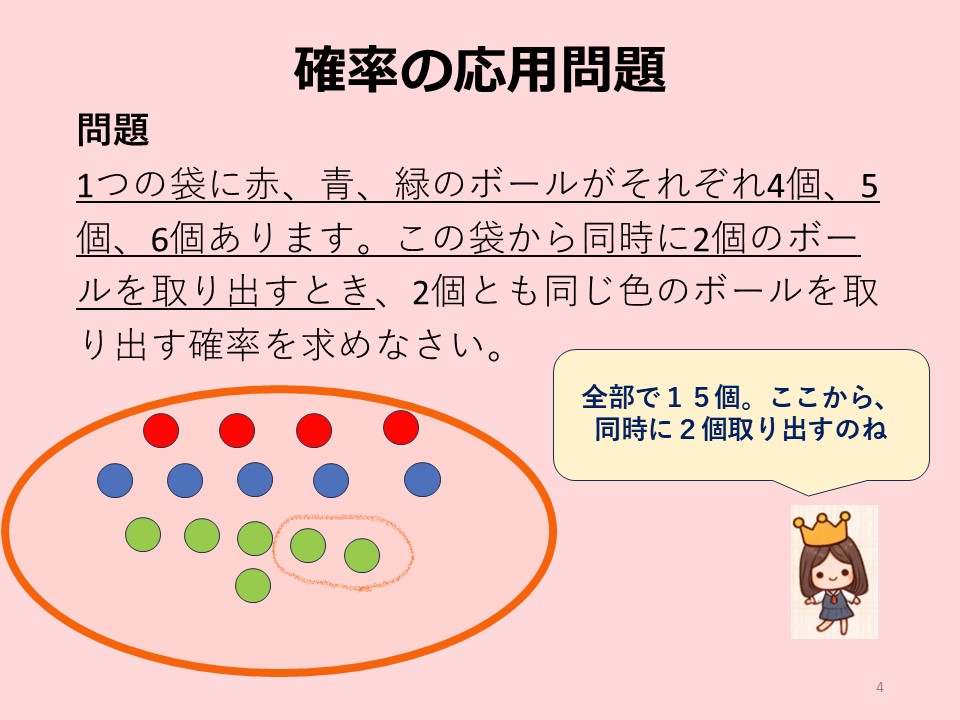
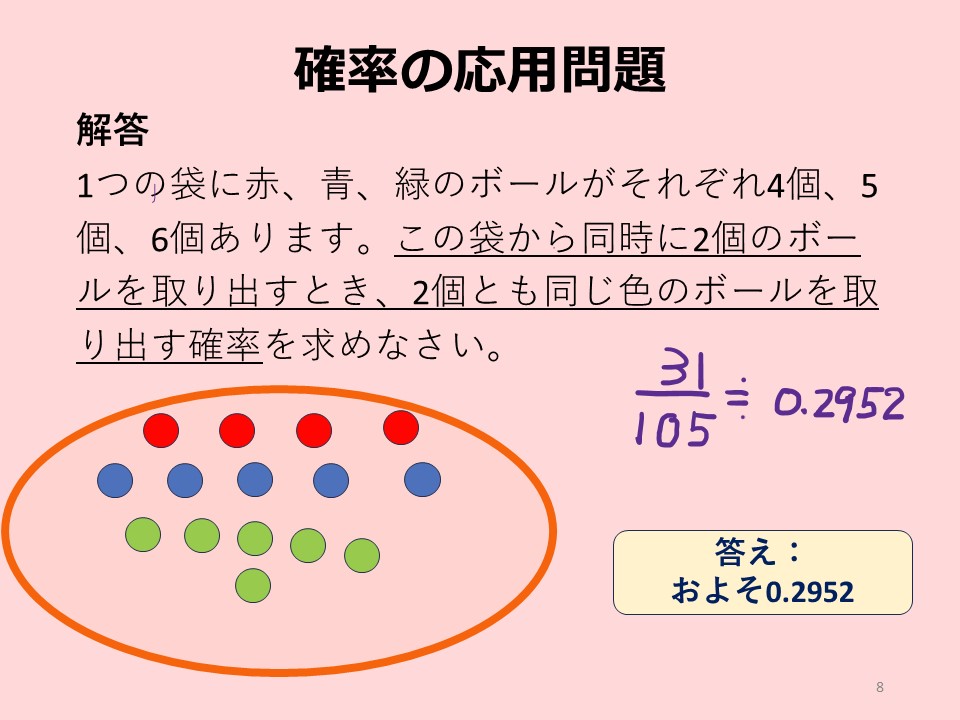
1つの袋に赤、青、緑のボールがそれぞれ4個、5個、6個あります。この袋から同時に2個のボールを取り出すとき、2個とも同じ色のボールを取り出す確率を求めなさい。

まず、問題文を絵で描いてみましょう

その2個には、いろいろな組み合わせがあるよね
例題 解き方①
それでは、スライドを見ながら一緒に解きましょう。
① 袋には合計で 15個のボールがあります。
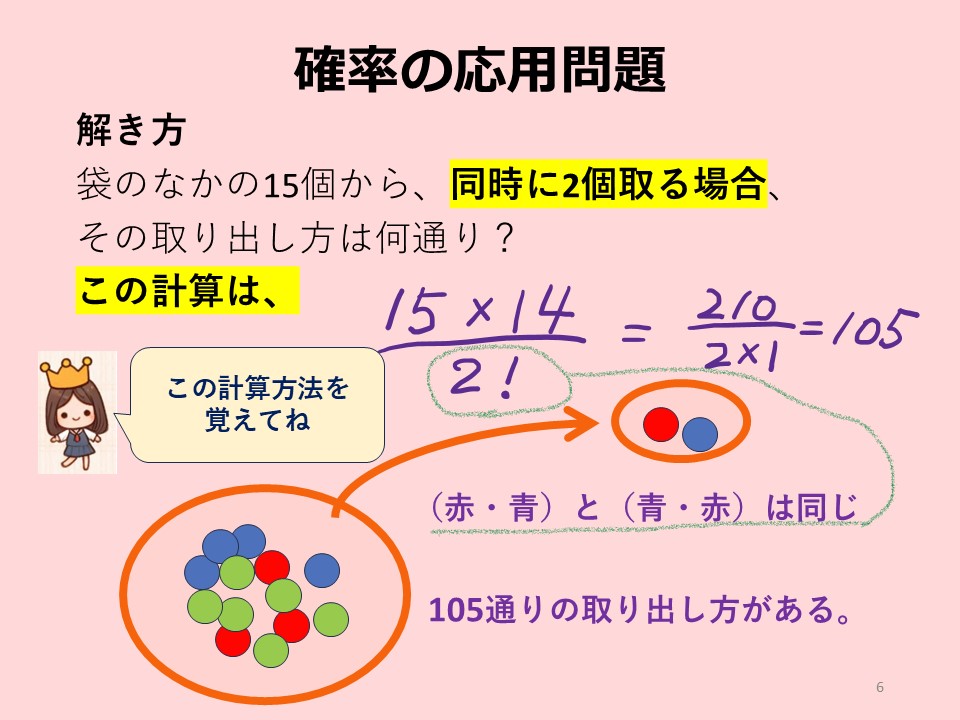
② まず、2個のボールを取り出すときの全ての組み合わせの数を求めます。
それでは、同時に2個のボールを取り出す場合の数を求めましょう。それは、下のスライドのように組み合わせの公式を使います。この公式の使い方を、例題を用いて説明します。
公式の使い方
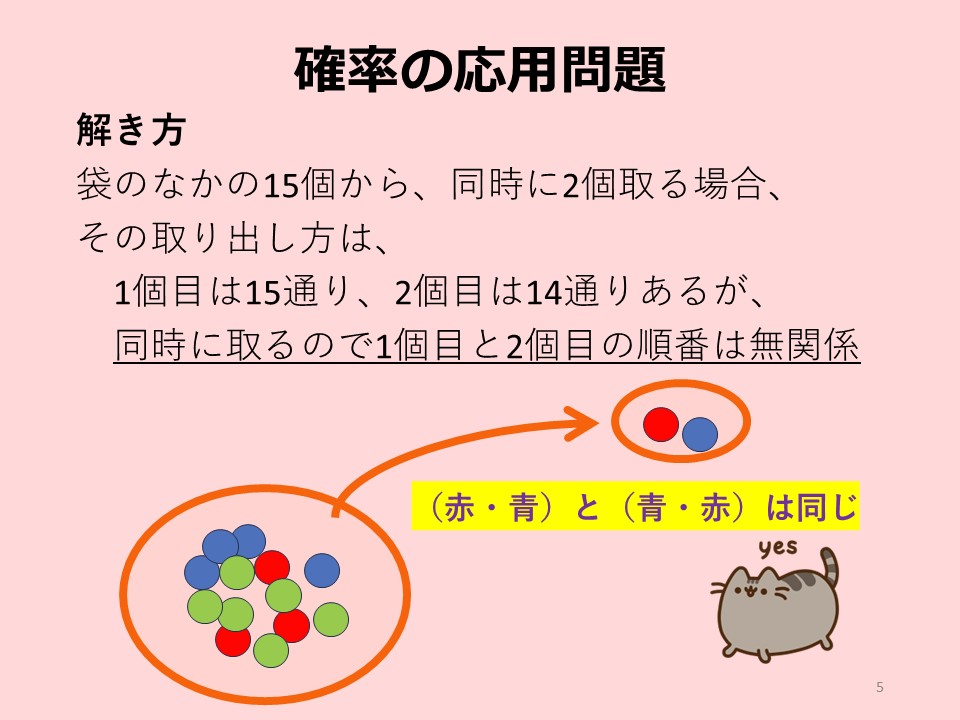
袋から2個取り出す場合の、ボールの組み合わせは15(1個目)×14(2個目)通りである。しかし、同時に取り出すということは、1個目と2個目の組み合わせは、例えば、(赤・青)と(青・赤)では、「どちらも同じ組み合わせ」を意味する。そこで、このような場合、(15×14)を(2!=2×1)で割ることで、15個から同時に2個取り出す組み合わせが計算できる公式を用いる。
つまり、同時に複数個を取り出す際の組み合わせの数の計算は、この公式を使えばいいのです。
例題 解き方②
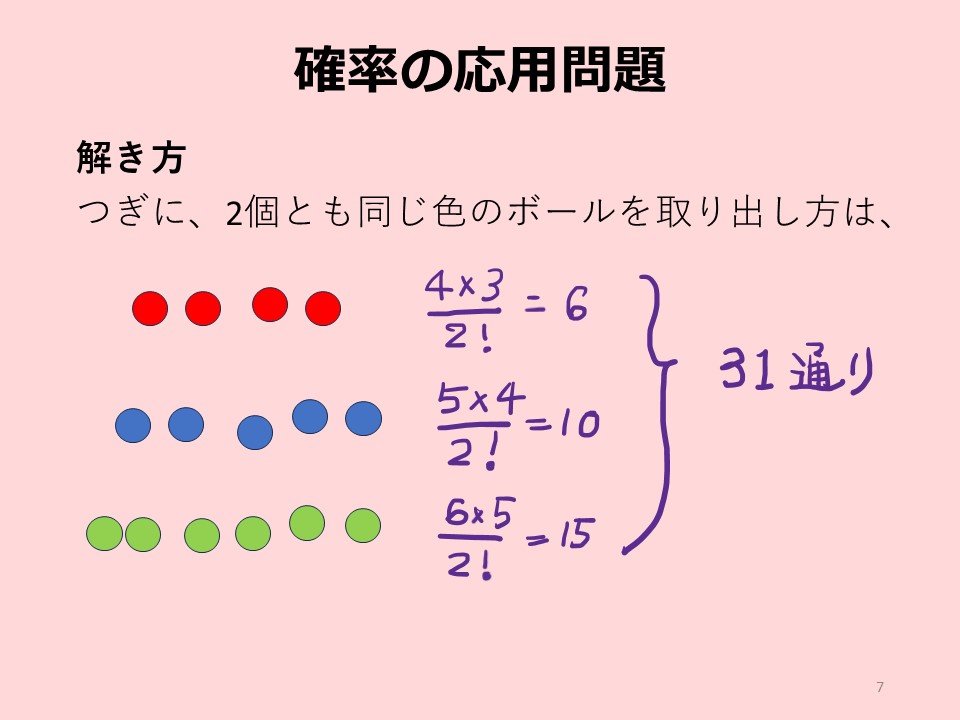
つぎに、 それぞれの色のボールが2個とも同じ色になる組み合わせの数を求めます。これも、同時に2個のボールを取るので、公式を用いて計算します。例えば、赤ボールを同時に2個取り出す組み合わせの考え方は次のとおりです。
「赤ボールは、全部で4個。ここから2個取り出す場合は、4(1個目)×3(2個目)通りの組み合わせがあるが、同時に取り出すので、例えば、(赤①・赤②)と(赤②・赤①)は同じ組み合わせを意味する。したがって、この場合も公式で計算し、2個ともに赤ボールの組み合わせの数は6」
また、具体的に書き出すと、(赤①・赤②)(赤①・赤③)(赤①・赤④)(赤②・赤③)(赤②・赤④)(赤③・赤④)で6通り、公式の計算どおりです。さらに、青ボール、緑ボールそれぞれ計算して求めます。
2個とも赤ボールの組み合わせの数は6、青ボールは10、緑ボールは15でした。したがって、同じ色どおしの組み合わせの数は、つぎのようになります。
6+10+15=31(通り)
例題 解答
最後に、同じ色のボールを取り出す確率を求めます。この確率は、同じ色のボールを取り出す組み合わせの数(31)を、全部の組み合わせの数(105)で割ったものです。
これで、2個とも同じ色のボールを取り出す確率は、約 0.2952(31/105)です。
間違えやすいポイント
ところで、例題の間違えやすいところは、各色のボールの組み合わせを求める際も、組み合わせの公式を使うことです。しかし、つい、忘れがちです。つまり、全ての組み合わせと同じ色の組み合わせをそれぞれ正しく計算することが重要な例題でした。これが、複合的な確率ですね。
類題
1つの袋に赤、青、緑のボールがそれぞれ4個、5個、6個あります。この袋から同時に3個のボールを取り出すとき、3個とも同じ色のボールを取り出す確率を求めなさい。
答えは、こちら
確率の学習方法 ワンポイントアドバイス
それでは、ここまで頑張ったみなさんに、効果的な学習方法をいくつかご紹介します。自分に合いそうな方法を取り入れてくださいね!
基本問題を反復的に解く
1 基本的な概念の復習 → 確率の定義や計算方法をしっかり復習する。
2 例題 → 基本問題集の例題を解くことで、確率の計算に慣れる。
標準~発展問題に取り組む
1 条件付き確率に挑戦 → 第3回のような問題からスタートし、徐々に難易度を上げる。
2 応用問題 → 問題文をよく読み、条件を正確に把握して解く練習をする。
 |
動画やオンライン教材を活用する
自宅学習で頑張っている人に特におすすめなのが、動画やオンライン教材です。例えば、 通信教材では、利用者へのサポート動画を配信していることがあります。このサービスが利用できる人は、ぜひ、視覚的な学習も取り入れましょう。こういった動画は、自宅で好きな時間に、繰り返し見られるのでよく理解できますね。
友達と情報交換する
ところで、なぜかやる気が出ない日もありますね。そんな時は、友達と一緒に問題を解いたり、解説しあったりすることで、お互いに刺激を受け、いっそう理解を深めることができます。もちろん、一緒に先生に質問に行くだけでも気分が違ってきますよ。学習継続には、よい気分転換が必要ですね。
まとめ
第3回からここまで読んだみなさん!いかがでしたか? 確率の概念を理解し、公立高校入試に備えるためには、基本的な問題から応用問題まで幅広く取り組むことが大切です。今回紹介した例題と解説を参考に、日々の学習に役立ててください。では、また💛
こちらの記事も、例題で確率を説明しています。 答え:約 0.0747



