こんにちは、中学2~3年生のみなさん! 公立高校入試に出そうな数学シリーズ第5回は、「統計」の基本について、わかりやすく図説します。最近の入試で注目のデータ活用につながるテーマですね。基本例題を一緒に解いて、焦らずに入試対策を進めましょう!中1のみなさんも、ぜひ、のぞいていってくださいね。

平均値とか中間値とか…

データの解釈ってどうするの?
基本的な統計の概念
まずは、統計の基本から始めましょう。つまり、平均値、中間値、最頻値の求め方と意味合いを押さえましょう。
平均値
はじめに、平均値です。これは、データの合計をデータの数で割ったものです。例えば、テストの点数が70点、80点、90点の場合、平均値は (70+80+90)÷3 = 80点です。
また、データの平均値は、全体の傾向を示しますが、極端な値のデータが含まれる場合は、その影響を受けやすい値でもあります。例えば、先ほどのテストの点数にもう1人(30点)を加えて平均値を求めると、(70+80+90+30)÷4 = 67.5点です。データ全体の傾向が変わってみえますね。
中間値
つぎに、最小のデータから順に並べたとき、中央に位置する値です。これを中間値(中央値)といいます。
もし、データ数が奇数(例えば、3個)なら、この中央(この場合は2番目)の値が中間値です。また、データ数が偶数の場合は、中央に位置するの2つのデータの平均値が中間値です。

おっと、データ数によって求め方が違うんだね
最頻値
最後に、最頻値を理解しましょう。最頻値とは、データ全体を見渡した時に一番よく出現する値のことをいいます。例えば、70点が2回、80点が1回、90点が2回出たなら、最頻値は70点と90点です。このように最頻値は1つの値とは限りませんね。

正しく並べて、データ全体をよく見ないとね

これで基本は、バッチリ!
例題
それでは、例題を一緒にやってみましょう。
平均値、中間値、最頻値の計算

平均値 解答・解説
まず、平均値を求めて説明しましょう。

中間値
つぎに、中間値を求めます。データは、最小値から順に8個が並んでいます。中間値は、データ全体の中央に位置している値ですが、データ数が偶数のときは計算が必要でしたね。

最頻値
最後に、最頻値を説明しましょう。データセットに同じ値が頻繁に出てきませんか?最頻値は、全データ中にもっとも数多く出現する値をいいます。

グラフの作成と解釈
今まで、データ全体の平均値を求めたり、順番を並べ替えて中間値や最頻値を求めながら、データを観察してきました。しかし、このデータの状況を知るためにはもっと良い方法があります。
つぎに、データを視覚的に表現する方法を学びましょう。
度数分布表
まず、データをカテゴリー(階級)別に整理して、各カテゴリーの出現頻度(度数)を表にまとめたものが、度数分布表です。この表を作ることで、どのカテゴリーが一番多いか、データの分布状況がわかります。
ヒストグラム
つぎに、ヒストグラムを作ってみましょう。ヒストグラムとは、度数分布表を棒グラフの形にしたもののことです。つまり、データの分布状況を棒の長さで表した統計グラフです。
したがって、ヒストグラムを使えばデータの特徴や傾向を簡単に把握することができます。

これは統計資料でよく見るね
例題
それでは、基本の統計用語がわかったので、つぎに、実際に手を動かして問題練習してみましょう。また、公立高校入試対策としても、このような例題に慣れておくことをおすすめします。
データの整理とグラフの作成
まず、この例題を一緒に解きながら、データの整理やグラフの作成をしてみましょう。
解答のポイント
① データを小さいものから順に並べる。(この例題はすでに並んでいる)
② 身長に着目し、カテゴリー別にデータを整理する。

度数分布表とヒストグラム
つぎに、例題の度数分布表とヒストグラムを自分で描いてみましょう。
いかがですか? 下のスライドのような表と棒のグラフが描ければOKです。
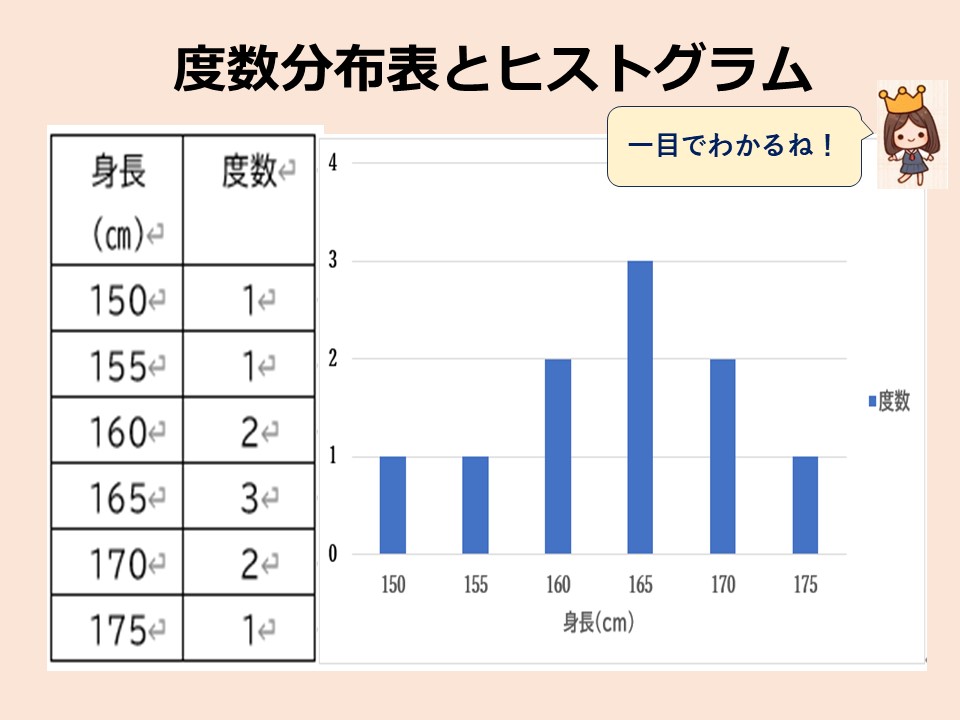
データの特徴
それでは、このヒストグラムで、例題のデータの特徴を説明しましょう。
説明
① 多くの生徒の身長が165cmに集中している。(棒グラフが最も高い)
② データの範囲は150cmから175cmで、ばらつきが比較的小さい。
間違えやすいポイントの確認
ところで、統計の問題は、基本の概念を理解していれば正解率が高いのですが、データの並び替えなどをしているうちにミスをしがちです。このようなケアレスミスで、自分だけがテストで得点できなかったらとても残念です。
また、公立高校入試では難問奇問が出題されない分、ケアレスミスをしないことが大切であると別の記事でお伝えしましたね。ですから、普段からつぎのポイントをよく意識して問題練習することが大切です。公立高校入試の極意は、ミスを減らして、スピードアップ&見直しですね。
注意のポイント
① 正しいデータの並べ替え:小さい値から順に並べ替える。並べ間違い、書き間違いに注意
② 正しく計算:データを丁寧に確認、確かめ算をする。
③ 完成した表やグラフの見直し:ミスの発見、修正
応用力の強化
近年、集めたデータをどう活用するかということが、ますます注目されています。つまり、公立高校入試でも、統計やデータ活用に関する出題は当分続きそうです。このテーマでは、応用力を身につけるための問題練習が大切です。基本的な統計概念を、さまざまな状況で活用できるように、数多くの応用問題に挑戦してみてください。
 |
まとめ
いかがでしたか? 今回は、統計を基本から見てきましたね。ですから、「統計がわかってきたよ~」という人が少しでもいてくれたらうれしいです。管理人も、公立高校入試に出そうな例題をもっと探してきますね。
でも、もしかすると、「やはり、わからない…」という人がいたかもしれません。その人には、お役に立てなくてごめんなさい。その場合は、まず、お友達や先生に悩みを話してみましょう。話しているうちに、解決方法が見つかることがあります。
しかし、それでも解消しない時は、早めにおうちの方に相談し、個別指導を受けるとよいかもしれません。なぜなら、わからないまま学習しても不安が募るばかりだし、やはり、自分に合う学習指導者と一緒に、困難を乗り越える方が、問題の解決は早いと思うからです。
ぜひ、ここで立ち止まらずに、さらに、似ている問題を探して練習してください。そうすれば、「本当に統計がわかったな~」と実感できますよ。 では、また💛



