こんにちは!「数学がちょっぴり苦手でも大丈夫!分かりやすい数学シリーズ」をお届けします。今回は、公立高校入試にもよく出てくる「一次関数」の基礎について一緒に学びましょう。
少しずつ理解を深めていけば、苦手意識もきっと克服できます。一緒に、やってみましょう。

高校入試に出ちゃうの?

中2の「一次関数」も?
直線のグラフとその方程式
公立高校入試では、直線のグラフの基本的な性質とその方程式の形がよく出題されます。これは、中学2年の学習範囲です。
このように、中2の学習範囲から出題があると知ることで、普段の学習にグッと身が入りますね。
一次関数は中学数学の基本。この理解が苦手意識克服のチャンスです。
また、解き直しノートがある人は開いてくださいね。そこに一次関数の記述があれば、以前、解けなかった問題があるということですよね。ここでまた問題を解けば、一次関数の記憶が更新します。
学習記憶は、少し間をあけて繰り返すことで定着します。
例題
では、つぎの例題を見てください。例題1と2では式が違います。
つまり、この2つの式の、どこが同じで、どこが違うのかを知ることがポイントです。

一次関数の式から分かる情報
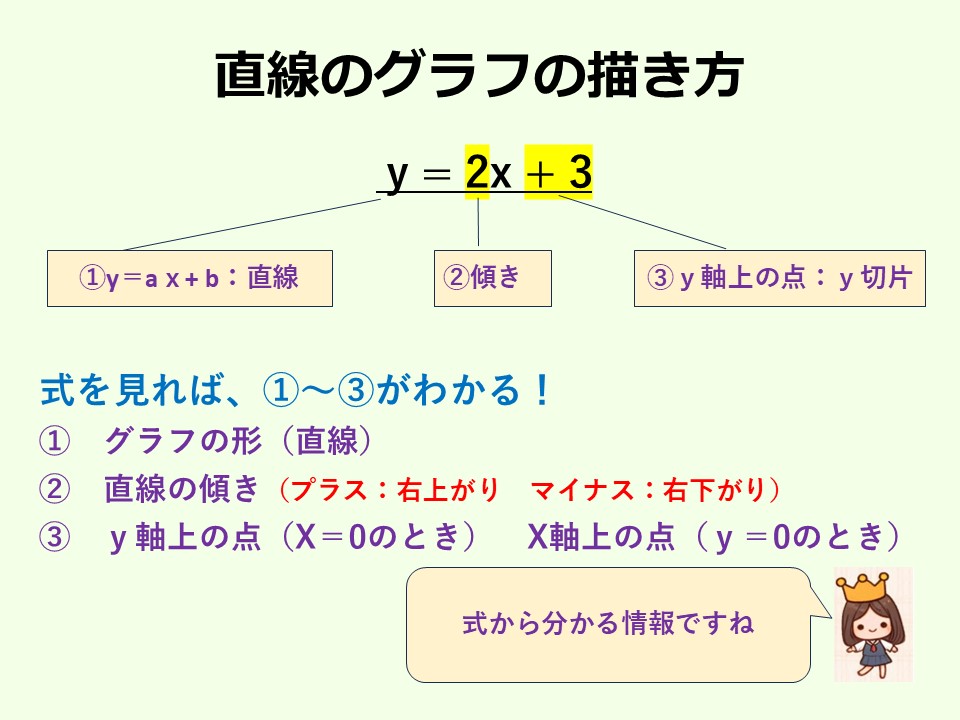
まず、一次関数の式から分かる情報を整理しましょう。次のスライドをみてください。
このように、式をみることで、①グラフは直線になる ②傾き方 ③y軸上の点の位置が分かります。①~③を理解すると、グラフをどのように描けばよいかが見えてきます。
グラフ
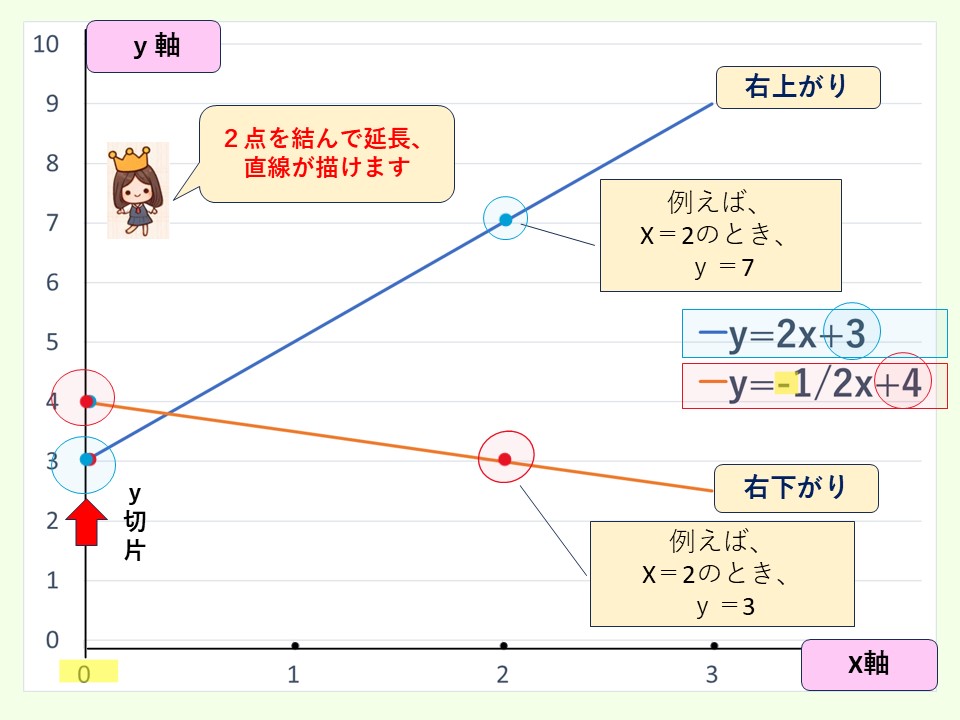
それでは、例題1と2のグラフを描いて見比べてみましょう。
直線グラフの留意点と簡単な描き方
① 直線を描くために、最低2点の位置を知ることが必要。
② 式から、y軸上の点の位置はわかる。(y切片)
③ もう1点の位置を計算で求める。
例えば、x=2のときのyの位置は、例題1と2ではどこか。
④ ②と③の位置を結び、線を延長することで直線グラフが描ける。

描けた!

私も🎵
変数間の関係
つぎに、一次関数における変数xとyの関係性を理解しましょう。

例題のポイント
① xの値が変わると、それにつれてyの値がどのように変わるか。
② 式のxに具体的な数字(例題3は「4」)を入れ、その時のyの値を計算する。
③ 式のグラフは直線
④ y切片の位置
⑤ ②③④でグラフが描ける。
身近にある「変数間の関係」
「変数間の関係」というと難しそうですが、身近にはこのような関係がたくさんあります。
例えば、「比例」や「反比例」もそうです。
例えば、一定の速度で走るという条件で、「時速□㎞で走る自動車は、◇時間後、スタートから何㎞地点に到達するか」「スタートから〇㎞地点に到達するための所要時間は、時速□㎞で走る場合と時速△㎞で走る場合はどう変わるか」といった関係は、一次関数の式で表せますね。

こんな文章題、よくみかけますね
まとめ
一次関数は、方程式からわかる情報を整理してグラフが描けるようになれば基本知識はOKです。まず、教科書レベルの問題を繰り返し練習しましょう。一次関数のグラフの描き方がわからない場合は、友達や先生にコツを聞きましょう。
もし、わからないことが多すぎる場合は、基礎固めに時間をかける方が、結果として早く学習成果がでます。この場合は、指導者と一緒に取り組むとよいのですが。
わからないことを放置しないで、おうちの方に早めに相談してね。
お疲れ様でした!一次関数の基礎、しっかり理解できましたか?これからも一緒に数学を楽しく学んでいきましょう。次回は、これもよく出題される「平面図形」について探究しますので、楽しみにしていてくださいね。
では、また💛
家庭教師センターをお探しなら、かてきょナビ!※本記事は一部広告を含みます。



