中学生のみなさん、こんにちは! さて、今回は、公立高校入試に出そうな数学シリーズの第2回です。 中学2年までの学習範囲で「平面図形」に関する例題2題を一緒に解いて、解法のコツをつかみましょう。

平面図形も大事だね

中2のうちに復習しておこう💛
例題1:三角形の外角の性質
公立高校入試では、三角形の外角の性質に関する問題がよく出題されています。まず、例題1を一緒に解いてみましょう。
問題
△ABCの外角∠ACDが125度、内角∠CABが45度のとき、内角∠ABCの大きさを求めなさい。

まず、問題文を図に描いてみましょう
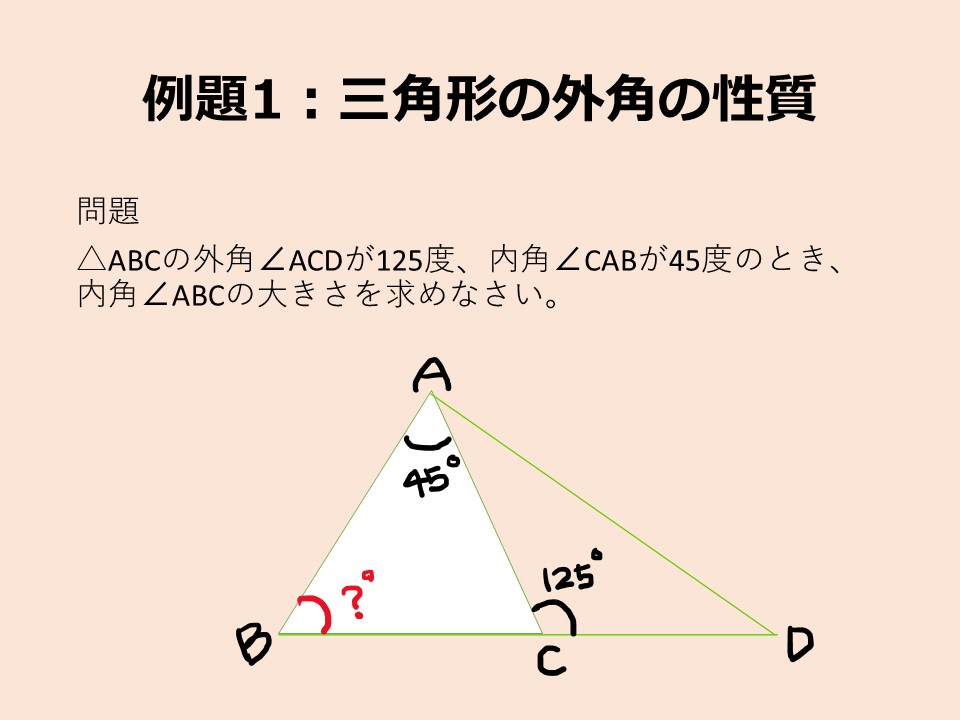
解説
ここでは、三角形の外角は、その三角形の内角の和に等しいという性質を利用します。つまり、外角∠ACD(125°)は内角∠CAB(45°)と∠ABC(?°)の和に等しいということですね。
解答
外角∠ACD = 内角∠CAB + 内角∠ABC
したがって、 内角∠ABC = 外角∠ACD - 内角∠CAB = 125 - 45 = 80
答え : 80°
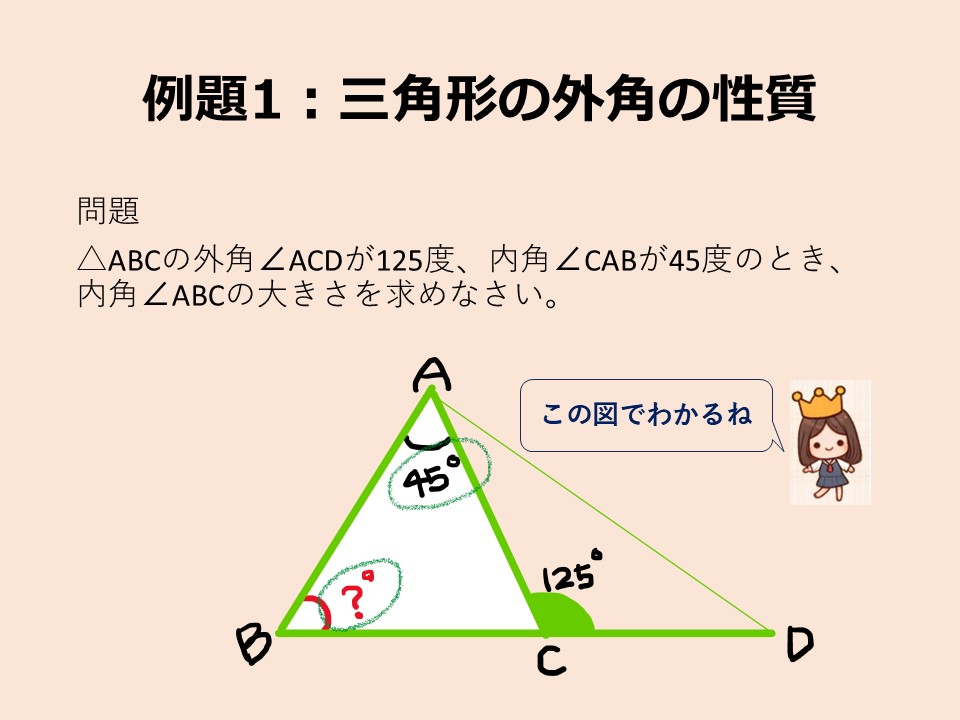
ワンポイントレッスン
もし、この問題を間違えた場合は、アドバイスを見ながら解きましょう。なぜなら、間違えた原因が分かれば、次は同じ原因で間違えないからです。
また、解き直しノートを見返しましょう。ひょっとすると、この例題は、以前に解き直した問題に似ていませんか? ここで、解き直しノートを見返すことで、解法の記憶を呼び戻しましょう。
ところで、「解き直しノートって何?」と思った人は、ぜひ、こちらの記事をみてくださいね。
アドバイス
1. 三角形の外角が隣接しない内角の和に等しいことを確認する。(スライド2枚目をみてね!)
2. 角度の計算ミスに注意する。基本的な計算力を鍛えよう。検算もしよう。
(検算のヒント : 三角形の内角の和は180°)
△ABCの内角はそれぞれ、45°、80°、55°である。△ABCの内角の和は、45+80+55=180
この計算で、内角∠ABC=80°は正しいことが確かめられる。
三角形の外角は、隣接しない内角の和に等しい。角度の計算では、ケアレスミスに注意する。
例題2:台形の面積
公立高校入試では、台形の面積に関する問題もよく出題されています。公式を用いて求める方法や、三角形2つを組み合わせる方法で台形の面積を求めることができます。それでは、例題2を一緒に解いてみましょう。
問題
台形の上底が8 cm、下底が12 cm、高さが5 cmです。この台形の面積を求めなさい。

これも、図を描かないとね
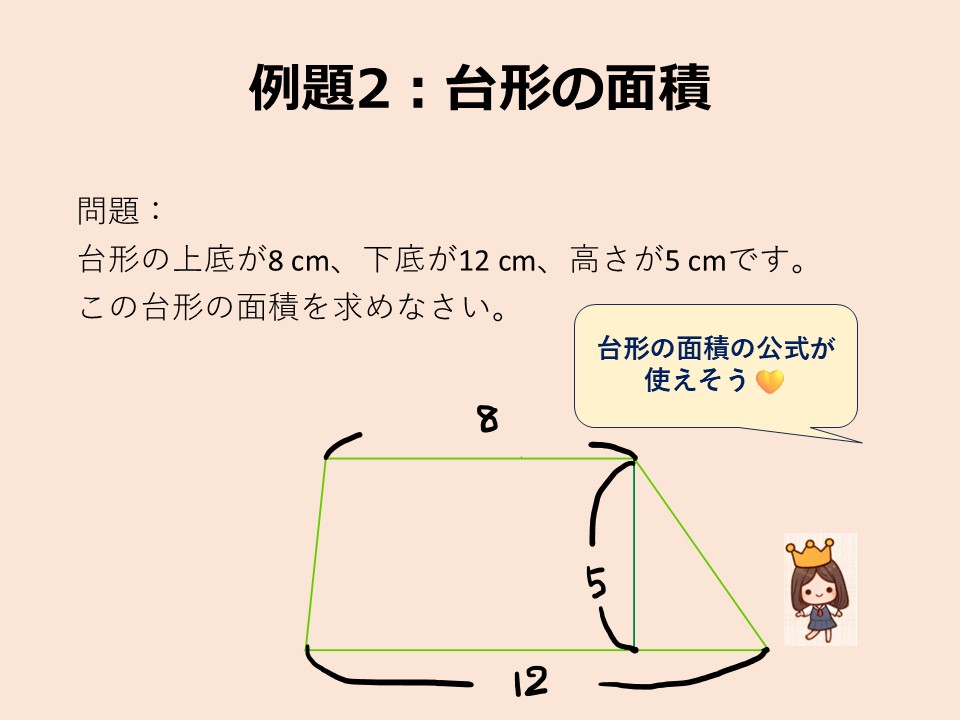
解説①
台形の面積は、「上底と下底の和に、高さを掛けて2で割る公式」で求めます。つぎのスライドを見てください。
この時に大切なことは、次の2つです。
① まず、台形の面積の公式を正しく覚える。
② また、問題文をよく読み、数値の単位がそろっていることを確かめる。
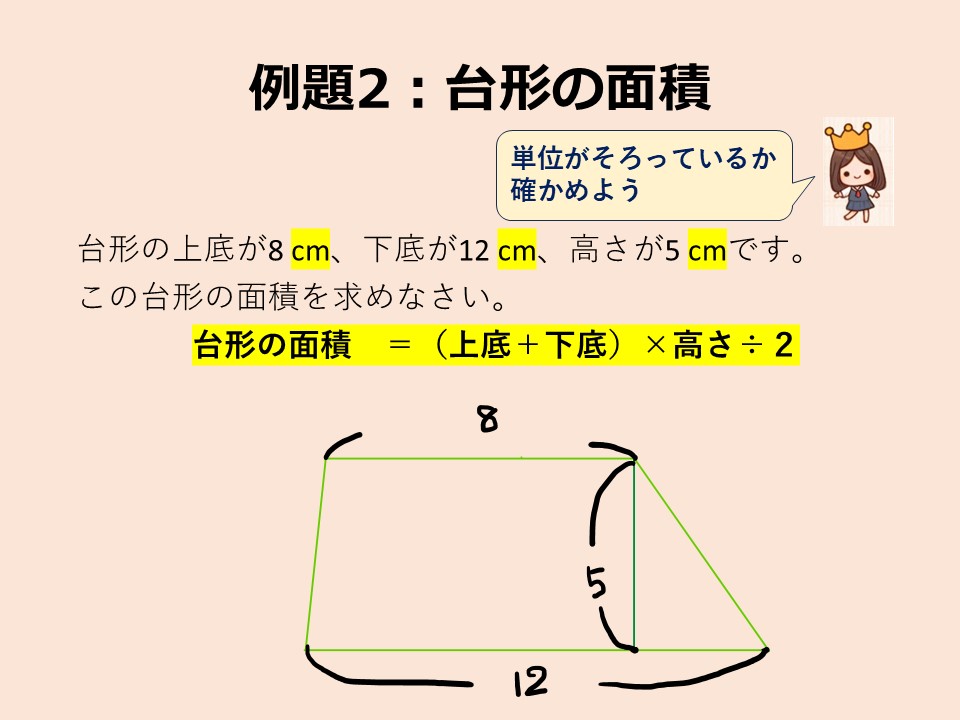
解答①
それでは、一緒に解答してみましょう。台形の面積の公式を用いれば、
台形の面積 = (上底+下底)×高さ÷2 =(8+12)×5÷2=50
答え : 50 ㎠
解説②
ところで、「三角形2つを組み合わせる方法」を用いて、台形の面積を求めることができます。こちらは、台形の面積の公式を忘れてしまった場合や、答えの検算にも使えるので便利です。
この時に大切なことは、次の2つです。
① まず、下のスライドのように上底と下底を線で結ぶ。
② すると、例題2の台形は、緑の線の三角形と青い三角形の組み合わせであることがわかる。
③ つまり、この2つの三角形の面積の和が台形の面積である。
2つの三角形の底辺はそれぞれ8㎝と12㎝で、高さはいずれも5㎝です。
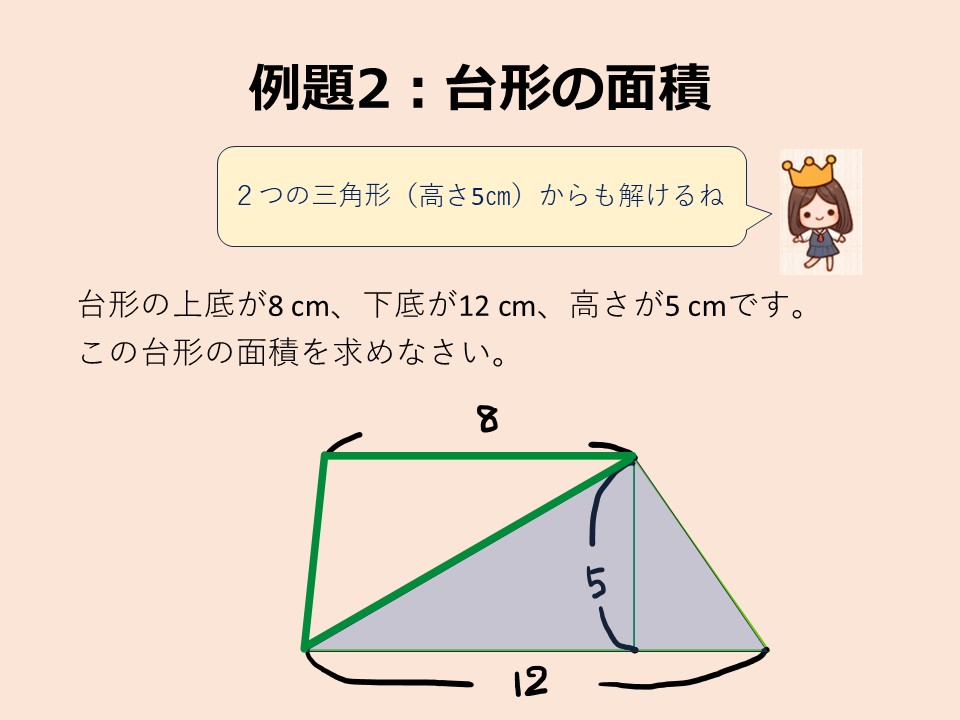
解答②
それでは、一緒に解いてみましょう。
緑の線の三角形の面積: 8(底辺㎝)×5(高さ㎝)÷2=20(面積㎠)
青い三角形の面積 : 12(底辺㎝)×5(高さ㎝)÷2=30(面積㎠)
台形の面積は、緑の線の三角形の面積 + 青い三角形の面積
したがって、 20+30=50
答え : 50 ㎠
ワンポイントレッスン
もし、この問題を間違えてしまった場合は、次の点に注意して、もう一度解き直しましょう。そうすれば、台形もこわくないですね。
アドバイス
1. まず、台形の面積の公式を正確に覚えているか確認する。
2. さらに、さまざまな台形の問題に取り組み、公式を使いこなす練習をする。
台形の面積の公式を正確に覚えているか確認する。さまざまな台形の問題に取り組み、公式を使いこなす。
 |
まとめ
公立高校入試では、中学2年生までの学習範囲から多くの問題が出題されます。なかでも、基本の「平面図形」の問題がよく出題されるため、ここで押さえておけば安心できますね。ですから、中2の学年末までに確実に復習しておくことをおすすめします。また、わからないところは、早めに友達や先生に聞きましょう。学習はタイミングが大切なので、必要ならば個別指導を受けることも検討するといいですね。
今回紹介した例題を通じて自分の理解度を確認できたら、ワンポイントレッスンを読み、教科書レベルの問題がすらすら解けるまで練習してみてくださいね。 では、また💛



