確率の応用問題の解き方！①　公立高校入試に役立つ実践ガイド

みなさん、こんにちは！今回は、公立高校入試に出そうな数学シリーズ第３回「確率」です。

確率の応用問題は、公立高校入試でもよく出題されるテーマの一つです。ですから、確率の基本的な概念と計算方法、そして応用問題に取り組むための解き方を図解します。

例題をみなさんと一緒に解きます。確率のコツをつかんでくださいね！

基本的な確率の概念

まずは、基本的な確率の概念をおさらいしましょう。

中２で学ぶ確率とは、ある事象が起こる可能性を数値で表したものです。

一般的には、次の式で表されます：　確率＝　成功する場合の数　/　全ての場合の数

この式でわかるように、確率を求めたいときは、「まず、全ての場合の数を書き出すこと」が大切です。

例えば、サイコロの「１」が出る確率は1/6です。

サイコロは、面ごとに「１～６」のどれか１つの目があります。サイコロは６面ですから、全ての場合の数は「６」。だから、サイコロを１回振る場合の「１」の目が出る確率は、1/6なのです。

確率の計算方法

それでは、つぎは、条件付き確率の例題を使って、具体的な確率の計算を一緒にやってみましょう。

条件付き確率

条件付き確率は、ある条件が成立したときに別の事象が起こる確率を求めるものです。でも、これではピンときませんよね。

また、例題を一緒にやっていきましょう。その前に「解き方のポイント」を示しておきます。

解き方のポイント
　①　図や絵で場合の数をとらえる。（頭の中で考えるのは無理です）
　②　ある条件の場合の数の計算方法

例題１：条件付き確率

３色（赤、青、緑）のボールが袋に合計１０個入っています。赤ボールが５個、青ボールが３個、緑ボールが２個です。赤ボールを引いた後、戻さずにもう一度ボールを引くとき、２回目に青ボールを引く確率を求めなさい。

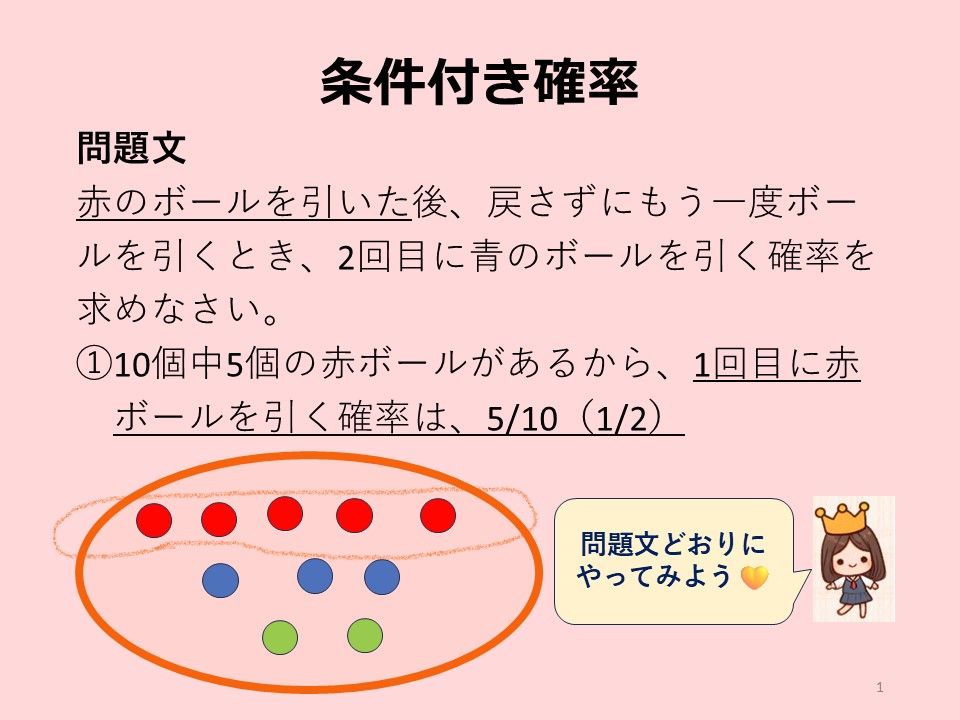
例題１：問題文の読み方・解き方

まず、赤ボールを引いた後、そのボールは袋に戻しません。したがって、袋には９個のボールが残ります。その内訳は、青ボールが３個、赤ボールが４個、緑ボールが２個です。

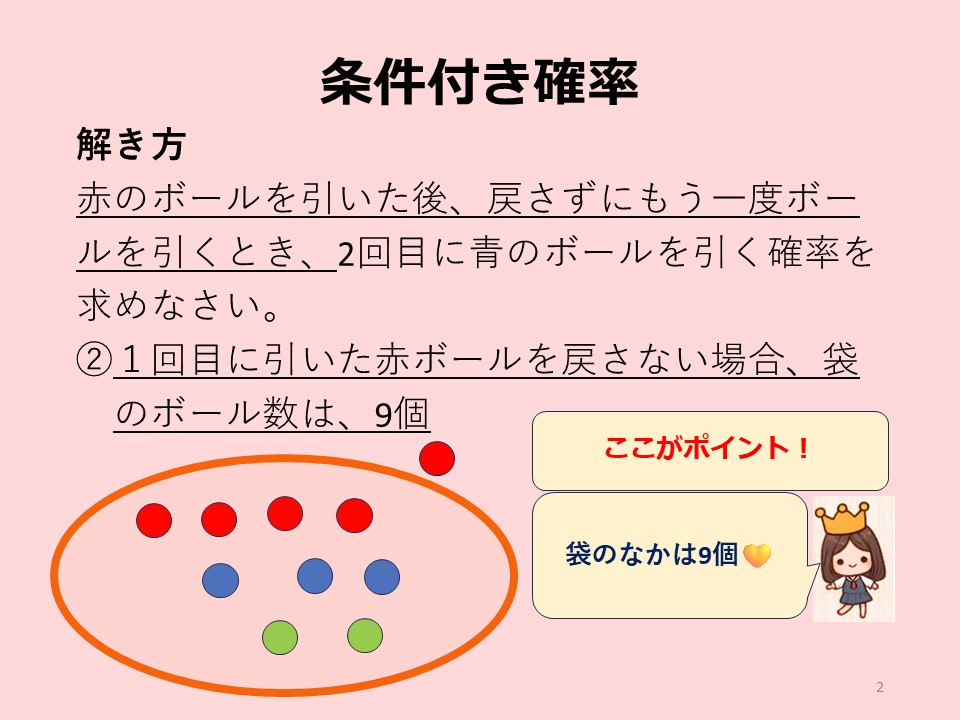
例題１：解答

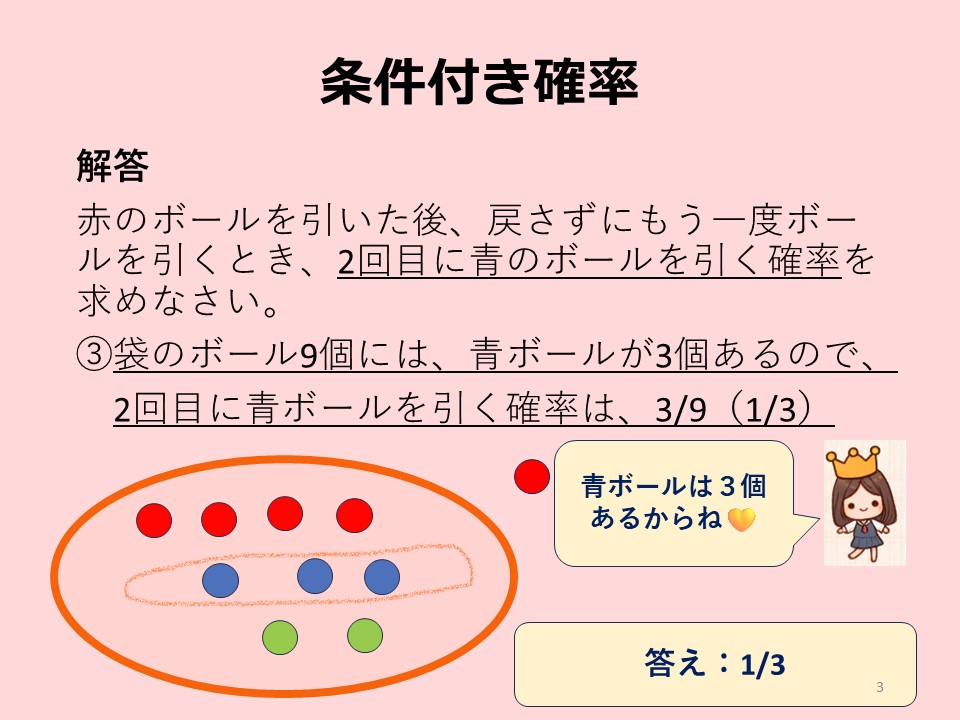
それでは、袋のなかの９個のボールから、青ボールを引く確率を計算してみましょう。

間違えやすいポイント
　①　赤ボールを引いた後、そのボールをどうするか。（袋に戻す？戻さない？どっち？）
　②　袋に戻さない場合、袋のなかのボールの総数が変わる。

つまり、この例題は、「１個目に赤ボールを引いたことでボール総数が１個減った」という条件下で、青ボールを引く場合の確率を求める問題です。

おうちの方へ
ひとりで考え込んでしまうと、確率の問題はとてもわかりにくいようです。問題文の状況を自分で絵や図にかけるようになるまで、だれかの助けが必要かもしれません。こまめに話を聞いてあげたいですね。

家庭教師センターをお探しなら、かてきょナビ！

※広告：A8.netを利用しています。

中間まとめ

確率の基本がわかると、条件付き確率がわかってきますね。ここで、タイミングよく問題演習を繰り返えせば、自分の理解度をもっと実感できますよ。そして、基本問題がスラスラと出来るようになったら、応用問題にも挑戦してみましょう。

しかし、もし、「数学が不安」「やはり、確率がわからない」と感じたら、その「悩み」は友達や先生に話してみましょう。話すことで頭の中が整理されたり、よい解消方法が見つかったりするかもしれません。

それでも解決できない場合は、早めにおうちの方に相談しましょう。学習の困難は長引かない方が早く解消するし、自分に合う指導者と一緒に取り組む方が確実だからです。

それでは、次回は、今回の続きで「確率の応用問題」を探求します。では、また💛

※本記事は一部広告を含みます。