こんにちは、みなさん!前回の第6回では、中2学習範囲の証明例題を取り上げました。 そこで、今回は、三平方の定理と円周角の定理に焦点を当てます。
それでは、証明が苦手な中2、中3のみなさん、公立高校入試に出そうな証明例題を一緒にやってみませんか?もちろん、中1のみなさんも大歓迎です。💛

三平方の定理と円周角の定理…

証明の文章が苦手かも
証明問題の解き方のポイント
はじめに、証明問題の解き方のポイントを簡単に押さえてみましょう。
図を描いて問題を理解
まず、問題文をよく読み、図を描いて視覚的に問題文を理解することが大切です。なぜなら、図を描くことで証明の順序が分かるからです。

図を描くって大切ですね
定理や公式を覚える
つぎに、証明に必要な定理や公式を確認しましょう。つまり「直角三角形といえば三平方の定理」「円周上の点と中心角といえば円周角の定理」といった具合に連想できれば、解答にグッと近づきますね。
したがって、公立高校入試によく出そうなこの2つの公式は、ぜったいに覚えておきましょう。
何を証明するのか
最後に、何を証明するかを図で確かめます。この時に、問題文から与えられる条件も図に描き込みましょう。
証明の順序を考える
さて、準備が整ったら、いよいよ、図を見ながら証明の順序や記述内容を考えます。
証明する
それでは、つぎの2つに注意しながら証明しましょう。
注意① 記述の仕方
まず、証明の文章で押さえておくことは、「数学の知識を用いて一貫して説明すること」です。ここで重要なことは、読む人にとっての分かりやすさです。
なぜなら、証明に至るまで仮定や数式が複数あるので、その関係性を説明しないと読み手には何を証明しているか分からないからです。これは、数学的な考え方と表現の問題全体にいえる特徴です。
そこで、証明の記述方法については、分かりやすさを含めた練習が必要になります。
そこで、おすすめなのが、「問題集の解説や解答の書き写し」です。この書き写しを読み返し、どのような順序で説明すると分かりやすいか、自分なりに考えてみましょう。
証明問題では、数学の知識に加えて、論理的な表現で読む人に説明することが大切
注意② 結論の確認
最後に、仮定から結論までを書きあげたら、今度は読み手側の立場で証明の流れをもう一度チェックします。
例えば、「~を~とする」「〇〇の定理の公式に~を代入すると~である」「したがって~である」といった言葉遣いは、読む人に分かりやすく伝える工夫です。これは証明文の記述パターンですから、積極的に使うとよいですね。
三平方の定理の証明例題
それでは、実際に例題で以上のポイントを試してみましょう。
例題1
問題
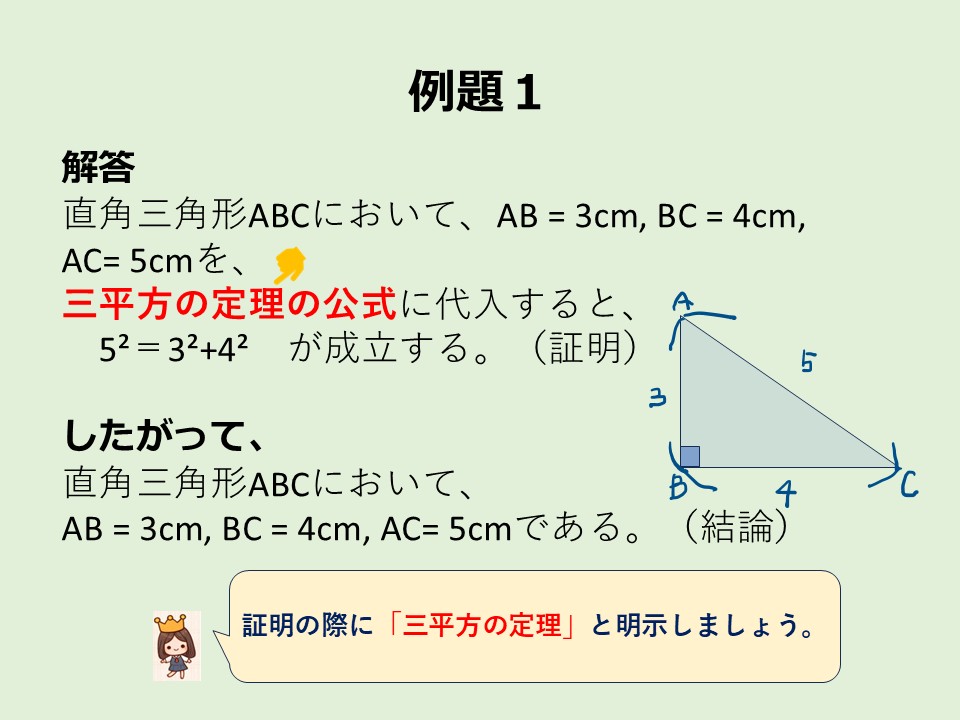
直角三角形ABCにおいて、AB = 3cm, BC = 4cm, AC = 5cmであることを証明せよ。
まず、解き方の流れを考えてみましょう。


こんな風に考えていけば、証明できそうですね。
例題1 解答
まず、直角三角形を描き、記号をつけます。すると、下のスライドの図になりました。
つまり、問題文に与えられたAB、BC、ACの長さに、「三平方の定理」の公式であるAC²=AB²+BC²の関係が成り立つかどうかを確かめればよいことがわかりますね。
さて、証明の文章は書けましたか? ここで、「証明する」の項と見比べて必要なことが記述できていればOKです。解答例(つぎのスライド)と同じ表現でなくても構いません。必要なことが順序よく書いてあれば正解です。
円周角の定理の証明例題
つぎの例題もやってみましょう。
例題2
問題
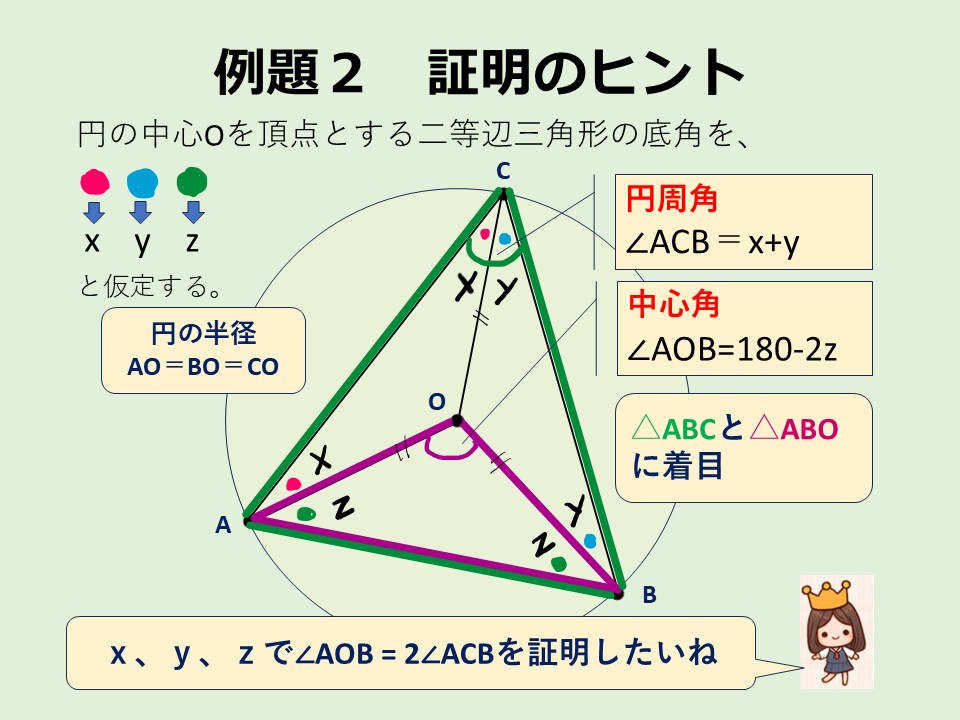
円Oの周上に点A, B, Cがあり、∠AOB = 2∠ACBであることを証明せよ。
ここで、解き方の流れを考えておきましょう。

例題2 証明のヒント
はじめに、この例題は、図を描いて理解することがとても重要です。下の図で証明の仕方を考えてみてください。
前提として必要な知識
① 円の性質
② 二等辺三角形の性質
③ 三角形の内角の和
④ 文字式と計算
例題2 解答
それでは、解答しましょう。この解答(下のスライド)では、2つの三角形の内角の和が180°であることを利用し、等式を立てています。そして、結論として円周角の定理が成立することを証明しています。では、読んでみてくださいね。

証明のヒントを使った場合は、だいたいこんな風になるのではないでしょうか?(表現方法は違っても大丈夫です)
まとめ
いかがでしたか?公立高校入試に出そうな数学シリーズ第6回と7回は数学的な考え方と表現の問題を取り上げました。これらは、数学の知識を用いて論理的に答える問題ですが、だいたい中2までの知識で対応できましたね。これは、大事なことです。
また、公立高校入試の傾向としても、中学3年間の基本知識の組み合わせ問題が多いようです。まずは、自分に合う問題集で基礎固めを始めましょう。
そして、中2までの基本問題集を早めに仕上げ、中3の授業と並行して過去問練習を繰り返すことをおすすめします。
 |
もし、悩みがあれば
ここで、教科書やワークなどがうまく進まない場合は、まず、学校の先生に相談しましょう。そして、それでもうまくいかない場合もあきらめは禁物です。
その場合は、自分に合う個別指導者と一緒に問題解決するという方法があります。
個別指導では、あなたの苦手の原因を客観的に分析し、学校とは別の視点で問題解消の早道を提案してくれます。学校の進度に遅れがちになっている場合は、おうちの方に早めに相談してみてくださいね。
「公立高校入試に出そうな数学シリーズ」はこの第7回までです。いつも、応援しています。
第1回はこちらです。
では、また💛



