こんにちは!今回は、高校入試に出題される「データの活用」問題の対策についてです。
さて、中学数学の「データ活用学習」は、中学1年から始まります。この学習には、数学の枠を超えた面白さがあります。もしかすると、この学習への取り組みで「数学好き」に転じるかもしれませんね。
中学数学の「データ活用学習」
以前の「データ活用学習」は、基本的な統計量(平均値、中央値など)や簡単なグラフ作成が主でした。しかし、2000年頃から、より高度なデータ分析や視覚化の学習が行われています。
具体的には、ヒストグラム、箱ひげ図、散布図などを使ってデータの分布や相関関係を学んでいます。これらは、社会統計やデータ分析の基礎なので、高校入試では頻出傾向です。

平均値、中央値、最頻値ってなんだっけ?
学年別「データ活用学習」
それでは、中学3年間の「データ活用学習」をつぎのスライドで見てください。これらの学習では、社会で役立つ「統計」や「データ」の知識が習得できるようになっていますね。


ヒストグラムや箱ひげ図って、ニュースでよく見るね
↓↓統計グラフでニュースがわかる!!↓↓
中高生新聞発行部数全国NO.1【読売中高生新聞】高校入試「データの活用」
それでは、高校入試で見かけるような問題を一緒にやってみましょう。
例題① ヒストグラム
まず、ヒストグラムを見てみましょう。
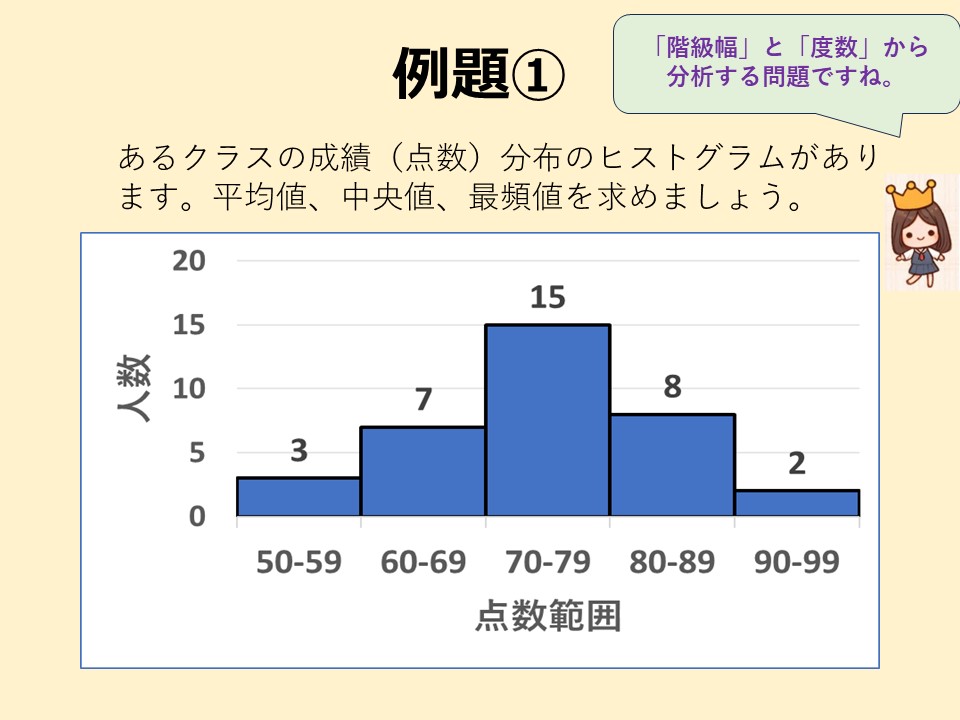
答えはこちら
例題① 解説
平均値
この例題では、生徒ひとりひとりの成績(点数)は示されていません。そこで、ヒストグラムの各階級(点数範囲)の中央値と度数(人数)に着目して平均値を求めます。
計算手順
①各階級の中央値を求める。
②各階級の中央値×度数を合計する。
③全度数で②を割る。
中央値
この例題の全人数は35人ですから、中央値は18番目の成績(点数)です。しかし、この例題では生徒の成績(点数)がわかりません。そこで、ヒストグラムの左から順に度数を累積していきます。すると、18番目の生徒の成績が「70-79」点の階級に入っていることがわかります。
計算手順
①70~79の中央値を求める。
最頻値
最頻値は、もっとも頻繁に現れるデータの値です。そこで、もっとも棒が高い(度数が高い)区間(点数範囲)に着目します。この区間が最頻区間です。
計算手順
①度数が最も高い区間(最頻区間)を探す。
②この区間の中央値を求める。
例題① まとめ
もし、生徒の成績(点数)がわかる場合はどうだったでしょうか。それならば、点数順に並べて中央値(18番目の点数)が特定できます。また、平均値と最頻値については、具体的な数値を調べて求めることができます。しかし、例題①は、その点が違いましたね。
例題①のヒストグラムから、つぎのように求められました。
平均値: 74.21 中央値: 74.5 最頻値: 74.5
例題②
つぎに、2つのグループのデータから、それぞれのグループの特徴を説明しましょう。
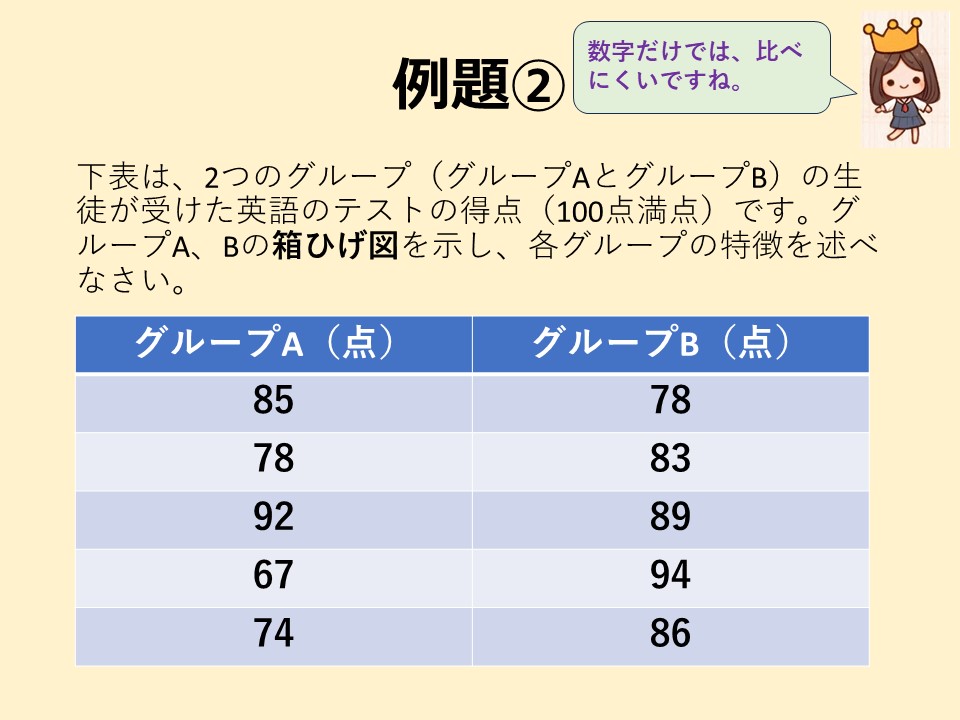
答えはこちら
例題② 解説
まず、箱ひげ図を描いてみましょう。この箱ひげ図を用いれば、2つのグループの成績分布の特徴を視覚的に比較できます。
作成手順
グループA
①データを小さい値から順に並べる: 67, 74, 78, 85, 92(データ数5で奇数)
②箱の部分:次のア~ウを示す。
ア:中央値(Q2):①の3番目の値(78)
イ:第1四分位数(Q1):67~74の中央値(70.5)
ウ:第3四分位数(Q3):85~92の中央値(88.5)
③ひげの部分
箱から最小値(67)と最大値(92)まで、それぞれ線を伸ばす。
グループB
①データを小さい値から順に並べる: 78, 83, 86, 89, 94(データ数5で奇数)
②箱の部分:次のア~ウを示めす。
ア:中央値(Q2):①の3番目の値(86)
イ:第1四分位数(Q1):78~83の中央値(80.5)
ウ:第3四分位数(Q3):89~94の中央値(91.5)
③ひげの部分
箱から最小値(78)と最大値(94)まで、それぞれ線を伸ばす。
例題② 箱ひげ図
いかがですか? 下の図は、表計算ソフトを使って描きましたが、もちろん、手描きでいいですよ。
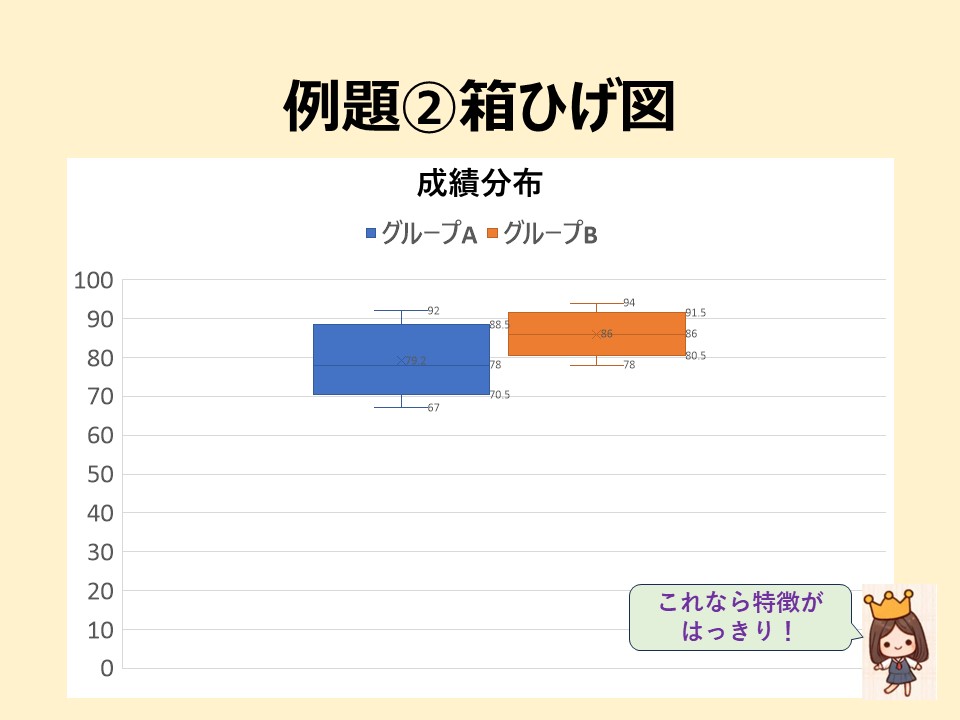
(箱の中の✖印は平均値)
例題② まとめ
それでは、この箱ひげ図を見て、各グループの特徴を説明しましょう。グループA(青)は、B(オレンジ)よりも広がった箱ひげ図で、Bの位置よりも下にあります。ですから、つぎのように説明できます。
グループA:成績のばらつきが大きく、最低得点と最高得点の差が広い。中央値は78で、全体の成績はやや低めである。
グループB: 成績のばらつきがやや小さく、全体的に高得点が多い。中央値は86で、全体の成績はグループAに比べて高めである。

この図を示すと説得力があるね
このように、箱ひげ図を用いることで、2つのグループの成績分布の特徴を視覚的に比較できます。もちろん、グループ数が増えても、データ数がもっと多い場合も同じ手法でデータ分析することができます。
「データの活用」問題と対策
2つの例題がすぐに解けなかったとしても、対策の方法があります。それに、中学生では、こういったデータ分析について体験の差があり、まだ、身近に感じられない場合があります。ここでは、自宅学習のサポートをご紹介します。
家庭内で基本的な統計を一緒に学ぶ
まず、教科書の例題を家族のだれかと一緒に解いて話し合ってみましょう。そうすれば、「データ」や「分析」がより身近に感じるでしょう。また、本人に学習サポートが必要かどうかも見えてくるかもしれません。
もちろん、教科書の例題でなくても大丈夫です。例えば、新聞記事のグラフからわかることを言い合ってみましょう。また、「お気に入りの曲の順位」「スポーツ選手の成績」などを記録し、そのデータを視覚化して分析するといったことも楽しいです。
このような家庭内のサポートがきっかけとなり、「データの活用」が身近に感じるようになれたらいいですね。
データの視覚化を楽しむ
データが収集できたら、つぎに、データの見える化をしてみましょう。統計の基本を学ぶ段階では、自分の手でグラフや図を描き、データ(数字)の意味合いを作業や視覚から理解することが大切です。
さらに、その基本がわかったら、ぜひ、パソコンやタブレットの表計算ソフトを用いて、データから様々なグラフを作ってみることをおすすめします。なぜなら、表計算ソフトを用いれば、多くのデータを瞬時に処理でき、しかも、簡単にグラフ化できる楽しさがあるからです。
データの視覚化は、たとえ数学が苦手だったとしても楽しめます。PCやタブレットの作図はかなり面白いので、これをきっかけに、数学の面白みに目覚めたらうれしいですね。

まず、自分で描くのね💛
PCで描いたグラフと比べてみようかな
学習環境の整備
ところで、こういった学習は、静かで集中できる環境の方がはかどります。この学習をきっかけに、静かで集中できる環境で学習するスタイルができるといいですね。
また、すでに自室で学習していても、「机周りの整理が悪くて集中できない」といった場合があります。このような場合は、物の配置を決め、机周りの整理整頓が大切です。さらに、学習カレンダーやスケジュール帳、文房具や定規セットといった必要な道具類も不足しないようにしましょう。
こういったことは、おうちの方に自室を一緒に見ていただいたり、整理整頓のアドバイスをしてもらうといいですね。
 |
 |
自宅学習のサポート
ここで、ご家庭内のサポートでは、ちょっと物足りない場合のサポートもご紹介します。
家庭教師
「データ活用学習」が遅れてしまった人におすすめなのが、マンツーマン指導の「家庭教師」です。家庭教師は「数学だけ」「データ活用学習の単元だけ」「この期間だけ」といった要望に応じてくれるのも魅力です。
さらに、家庭教師は、学習計画や進み具合を一緒に考えたり、励ましたりしてくれます。もしも、学習の遅れがある場合は、家庭教師と一緒に学習するのもいいですね。
また、訪問型ではなく、完全オンライン対応の家庭教師サービスもあります。いずれにしても、家庭教師は、「夜遅い」「遠い」といった心配が不要というのがうれしいですね。
通信教材
学習の遅れはなくても、学習量が足りていないことはありませんか?実は、どの科目にしても教科書のみで自宅学習するのは難しいです。なぜなら、教科書は先生の解説が前提ですから、解説も問題数も少なめだからです。これは、参考書と教科書の厚さを比較すればわかります。
ですから、自宅学習には、通信教材を取り入れると効率的に学力アップが見込めます。通信教材は、学習内容を徹底的に研究して作られています。そして、学校授業に合わせた内容を分割して送り、タイミングよく学習を促してくれます。これならば、参考書や問題集の最初の数ページしか見なかったという事態を防止できますね。
通信教材については、お試し教材や案内パンフレットを取り寄せ、費用やサポートについて比較するのがいいですね。例えば、授業レベルをしっかり学ぶならば教科書準拠の教材、授業とは別に「後戻りして十分に復習したい」「どんどん先取り学習したい」ならば無学年式の教材というように特色があります。
インターネット
学習計画を作ったり、学習レベルを調整したりできる人は、市販の参考書や問題集で計画的に学習すれば大丈夫です。このような人は、YouTubeなどの動画や学習解説や問題提供サイトも活用できるかもしれません。
ネットの視聴に時間を使いすぎてはいけませんが、取り上げられる問題の傾向がわかり参考になりますね。

その際は、ネット視聴の許可をおうちの方にいただきましょうね
おわりに
高校入試では、統計の基本から応用まで幅広く出題されます。受験期にあわてないように、早めに対策できるといいですね。特に、「データの活用」では、各学年で確実に力をつけていきましょう。この記事がデータ収集や分析の楽しさに目覚めるきっかけになればうれしいです。では、また💛



