こんにちは、数学の文章題が苦手な中学生の皆さん!文章題シリーズ第2回目です。
今日は「素因数分解」の文章題を一緒にやってみましょう。
このような問題を解くためのポイントと、解法のヒントを提供します。「計算はできるのに文章題になるとできない」のは、本当にもったいないですよね。

ところで、105を「素因数分解」できますか?


もちろん。計算は得意だよ。

小さい数から割って、かけ算の形にするのよね。
私もできた💛
文章題にチャレンジ
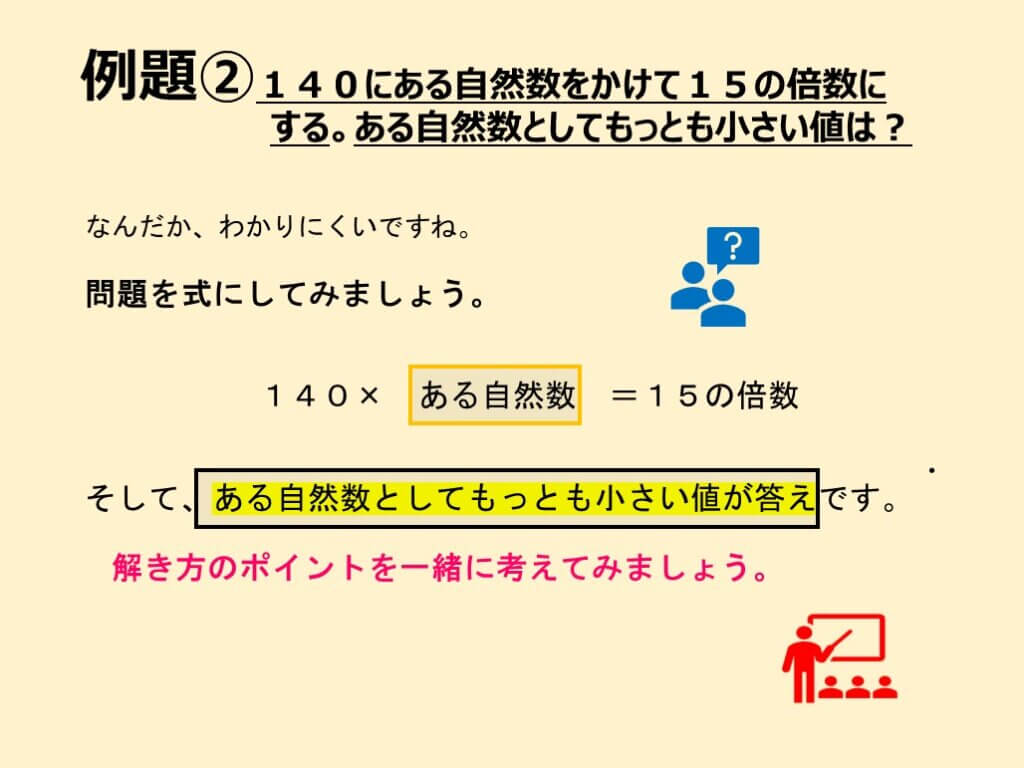

ん?どういうこと?問題の意味がわからないぞ。

書いてないけど「素因数分解」が関係ありそうね。
例題②のポイント
例題②のポイントは「140」という数と、「15の倍数」という条件です。これらの情報から、どのような自然数が条件を満たすのかを考える必要があります。
解法のヒント
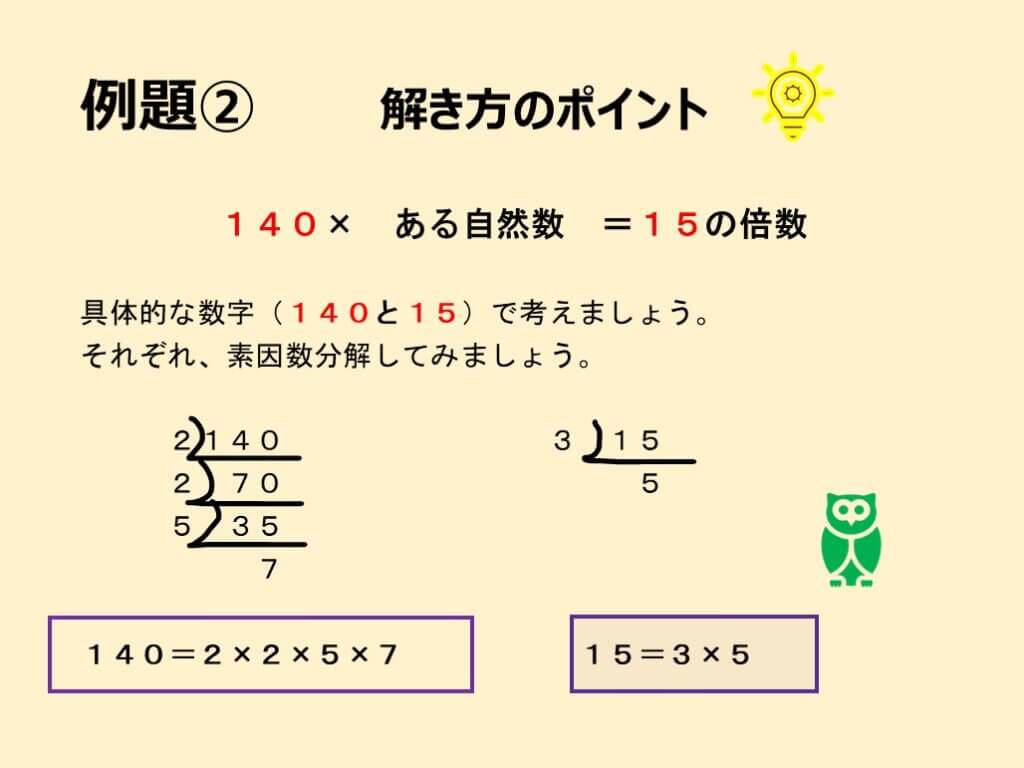
例題②を解くための一つの方法は、「素因数分解」を利用することです。
素因数分解とは、ある数を素数の積に分解することを指します。「140」と「15」をそれぞれ素因数分解するとスライド3枚目のようになります。
さらに、一緒に考えてみましょう。
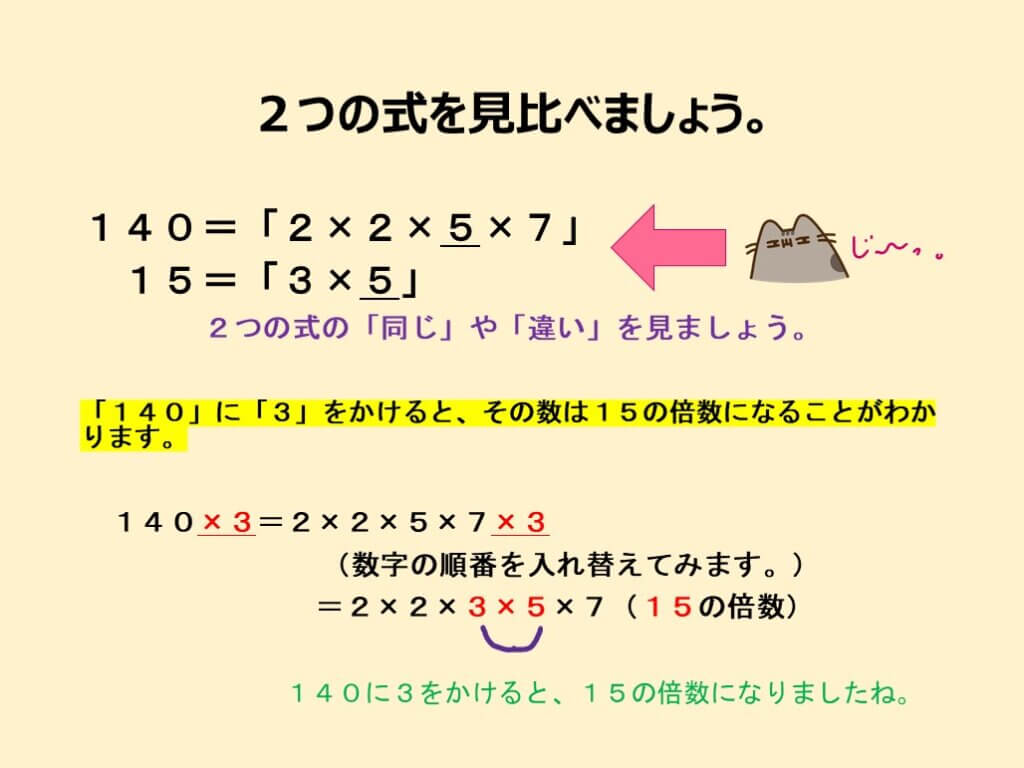
スライド4枚目を見てください。
例題②では、140にある自然数をかけて15の倍数にするためには、その自然数が少なくとも「3」である必要があります。なぜなら、140の素因数には「3」が含まれていないため、140に「3」をかけることで初めて15の倍数を作ることができるからです。 素因数分解で得た、その数の情報をよく見比べることで気づくことができますね。
解答する

したがって、この問題の答えは「3」となります。解答は、問題文を確かめて適切に答えてくださいね。
まとめ
数学の文章題は、問題の条件を理解し、適切な解法を選択することが重要です。
例題②では、「素因数分解せよ」とはありません。しかし、この手法を利用することで、140にどのような自然数をかければ15の倍数になるのかを見つけることができました。
数学の文章題が苦手な皆さんも、このような手法をどんどん使ってくださいね。似ている問題をみつけて練習し、問題解決のスキルを磨いていきましょう!

スライド1枚目の「105にある自然数をかけて、6の倍数になるもっとも小さい値はな~に?
またね💛
 |

.jpg)
-120x68.jpg)
-120x68.jpg)