【苦手克服！】一次方程式の文章題をスラスラ解く方法

文章題が少し苦手な皆さん、第1回から第3回までの文章題はいかがでしたか？数学の用語をはっきりとさせることは文章題の苦手克服に大切ですね。「文章題を一緒に解こう」シリーズ第4回目は、一次方程式です。問題文のどこに着目すべきか、つまり文章題の「目のつけどころ」や「解き方」が分かりますよ。

一次方程式とは何か？

一次方程式とは、変数が1つだけで、その変数の最高次数が1の方程式のことです。例えば、(2x + 3 = 7) という方程式が一次方程式です。次数が１で一次方程式、次数が２なら二次方程式といいます。

文章題への苦手意識を克服しよう

例題や似ている問題を練習することで、文章題への苦手意識を克服することができます。文章題では、まず問題文をしっかりと読み、解答として何が求められているのかを理解することが大切です。

例題　

一次方程式は、日常生活の中でよく使われる数学の基本的なツールです。さっそく、例題を一緒に解いてみましょう。問題文からできるだけ多くの情報を読み取りましょう。

お部屋の中でも、熱中症対策してますか？対策グッズはこちらからどうぞ。

問題文の読み方のポイント

問題文のポイントをとらえましょう。このように、要点に線を引いておくと解き方も見えてきます。
後から見直しするときにも便利です。

1. 周囲の長さ：池の周囲の長さが1680mであることを確認します。
2. 速度：父の速度が分速80m、母の速度が分速60mであることを確認します。
3. 求めるもの：父と母がはじめて出会う時間を求めます。

解法のヒント

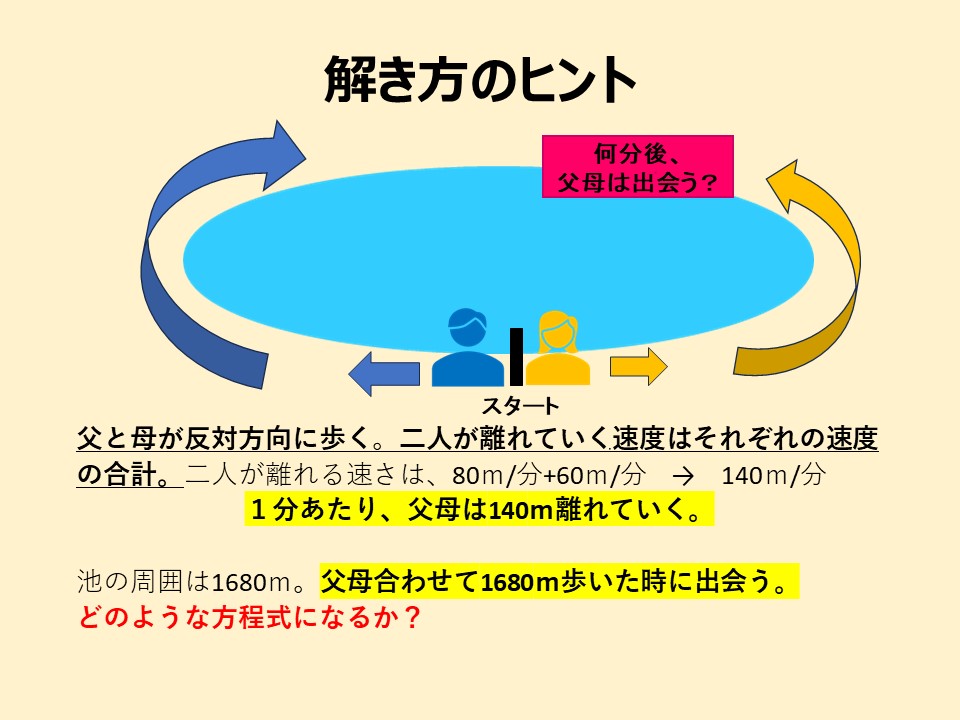
解法をまとめます。

1. 父と母が反対方向に歩くので、二人の速度を合計します。
2. 合計速度で池の周囲の長さを割ることで、出会うまでの時間を求めます。（距離、速度、時間の関係）

解答

このように、距離と速度と時間の関係を方程式にすればよいですね。

1. 父と母の合計速度は (80m/分 + 60m/分 = 140m/分) です。
2. 池の周囲の長さ1680mを合計速度140m/分で割ります。
3. (1680m ÷ 140m/分 = 12分)

したがって、池の周りを反対方向に歩き出した父母は、12分後に出会います。

検算の重要性と具体的な方法

解答を求めた後は、必ず検算を行いましょう。検算をすることで、計算ミスや問題文の読み間違いを防ぐことができます。今回の問題では、父と母が12分後に出会うことを再確認するために、もう一度、見直してみましょう。テスト時だけでなく、普段から検算の習慣をつけましょう。

検算の具体的な方法

検算の具体的な方法をまとめます。

1. 父の歩行距離：父は、分速80mで12分間歩き、その距離は(80m/分 × 12分= 960m) です。
2. 母の歩行距離：母は、分速60mで12分間歩き、その距離は(60m/分 × 12分= 720m) です。
3. 合計距離：父と母が歩いた合計距離は (960m + 720m = 1680m) です。

これは池の周囲の長さ1680mと一致するので、計算が正しいことが確認できます。

まとめ

このように、問題文を読み解いたり、解くための具体的な方法が理解できると、文章題への取り組みも面白くなりますね。例題を理解したタイミングを逃さずに、似ている問題を探してチャレンジしてくださいね。

探すのも楽しい！問題集はこちらからどうぞ。

こちらの記事もご参考にしてください。

中学生が苦手意識を克服できるようにサポートできればと思います。何か他に追加したい内容や質問があれば教えてくださいね！